lbed

2013/12/14からのアクセス回数 4689

Interface 2013/11から連載が始まった「実験で入門！音声合成のメカニズム」をLM4F120 LaunchPadで試してみます。

DACモジュールの作成 †

LM4F120 Lauchpadには、DAC（デジタルからアナログへの変換）モジュールが付属していませんので、 SPIインタフェースを持つ、12-bit DAC（デジタル・アナログ変換） MCP4922 を使用します。

MCP4922の使い方は、arduino/DACを試すを参照してください。

↑

MCP4922クラスを作成 †

MCP4922にアクセスするために、SPIクラスのサブクラスとしてMCP4922を作成します。

#include "MCP4922.h"

#define     HIGHT     (1)
#define LOW          (0)

MCP4922::MCP4922(PinName mosi, PinName miso, PinName sclk, PinName cs, PinName ldac)
     : SPI(mosi, miso, sclk), _ldac(ldac), _cs(cs)
{
}

void MCP4922::write(int value) {
     _ldac = HIGHT;
     _cs = LOW;
     SPI::write((value >> 8) | 0x30);
     SPI::write(value & 0xFF);
     _cs = HIGHT;
     _ldac = LOW;
}

void MCP4922::frequency(int hz) {
     SPI::frequency(hz);
}
↑

テストプログラムで動作を確認 †

SPIの通信には、SSI1を使用することにして、MOSI（PD3）, MISO（PD2）, SCLK（PD0）とつなぎます。 CS（PE1）, LDAC（PE2）としてJ3列のレジスタで揃えました。

LaunchPad-DAC-setting.png

TestMCP4922.cppは、以下の通りです。

#include "lbed.h"
#include "MCP4922.h"

int main(void) {
     // PD_2は使用していないので、未接続で実行
     MCP4922     mcp4922(PD_3, PD_2, PD_0, PE_1, PE_2);     // mosi, miso, sclk, cs, ldac
     // 16MHzにセット
     mcp4922.frequency(16000000);
     while(1) {
          for (int i=0; i < 4096; i+=4) {
               mcp4922.write(i);
          }
     }
}

こんなに簡単にノコギリ波の生成プログラムが出来上がります。

オシロスコープで生成された波形を見ると以下の様になります。

saw-wave.png

LM4F120 LaunchPadは、FPUが付いているので、sine波を計算するとどうなるか試してみました。

#include "lbed.h"
#include "MCP4922.h"
#include "math.h"
#define     PI     3.1415926
#define     SAMPLE 4096
#define     sin(x)     sinf(x)
 
int main(void) {
     // PD_2は使用していないので、未接続で実行
     MCP4922     mcp4922(PD_3, PD_2, PD_0, PE_1, PE_2);     // mosi, miso, sclk, cs, ldac
     // 16MHzにセット
     mcp4922.frequency(16000000);
     while(1) {
          for (int i=0; i < 4096; i+=4) {
               int sineValue = (int)(0xFFF*(1 + sin(2*PI*i/SAMPLE))/2);
               mcp4922.write(sineValue);
          }
     }
}

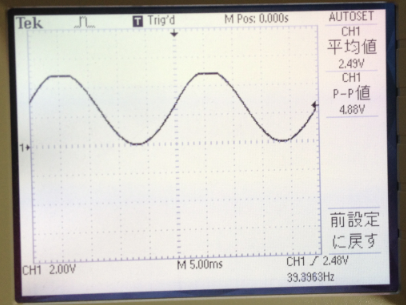
sine波の出力でも、39.39Hzで1024ポイント（1ポイント: 1/39.39/1024=0.025ms）を出力できています。 これなら音声合成で使用する8KHzサンプリング（1ポイント: 1/8000=0.125ms）データにも余裕で対応できます。 sine-wave.png

↑

第1回の課題 †

Interface 2013/11号の第1回目の課題をLauchpadで実験してみましょう。

↑

「あ」を合成するマイコン・プログラム †

Synthesisという関数を作成して、フーリエ係数から「あ」を合成してみるというものです。 ((例題では、サンプリングの不連続をちょっと補正するために、サンプリングデータの最初と最後の データの平均値を先頭の値にセットしています。))

母音の「あ」の合成には、以下のようなフーリエ関数を使っています。

$$ f\left( \frac{n}{8000} \right) = a_0 + \Sum_{k=1}^K \left( a_k cos \frac{2 \pi k}{T_0} n + b_k sin frac\frac{2 \pi k}{T_0} n \right), n =0, 1, …, N-1 $$

トップ   新規 一覧 単語検索 最終更新   ヘルプ   最終更新のRSS
SmartDoc